Faculty Statement
Research Vision
Control and Design of Disordered Materials Across Quantum to Continuum Scales
Disordered materials rarely operate at equilibrium. Structural glasses age over decades; colloidal suspensions jam and unjam under shear; and hierarchical, porous materials support electrochemistry under strong electrical currents. These materials underpin technologies from ultrastable metallic glasses, which are useful for their elevated mechanical stability at extreme conditions, to corrosion-resistant coatings, to recyclable soft matter for sustainable manufacturing. Despite their ubiquity and relevance, they cannot be harnessed through equilibrium thermodynamic principles alone, raising the following question: How do conditions out of equilibrium reshape the behavior of disordered materials? The answer lies in treating disordered materials as complex open systems, bringing us to my main goal:
As a faculty member, I aim to control and design disordered materials using theory and computation by engineering the flow of mass, energy, and momentum with the environment.
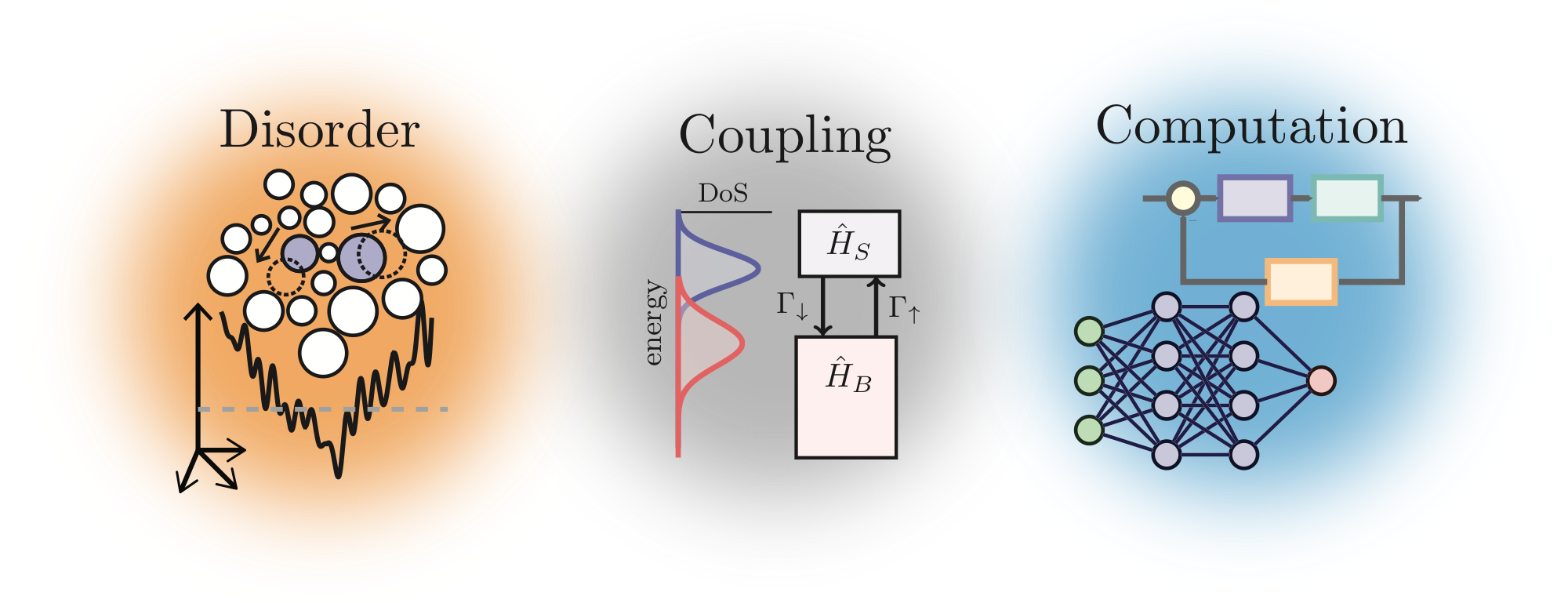
To this end, my research program unifies three foundational themes: Disorder, Coupling, and Computation:
- Disorder defines the inherent obstacle in materials design due to rugged energy landscapes that trap materials in unwanted metastable states
- Coupling provides control via mutual exchange with an environment that actively participates in the dynamics, e.g., reservoir of electrons, electromagnetic fields, or hydrodynamic flows
- Computation defines the methodology—multiscale in nature, spanning the quantum to continuum scales: electronic-structure theory, molecular dynamics, continuum-mechanics modeling, machine learning, and optimal control theory
This research program is structured around three thrusts:
- Thrust 1: Machine Learning for Ab Initio Electrochemistry. Developing theory, datasets, and ML models for molecular dynamics at electrochemical interfaces, enabling active-learning design of corrosion-resistant materials for extreme aerospace environments.
- Thrust 2: Polaritonic Engineering of Supercooled Liquids. Using quantum and classical light-matter control to engineer ultrastable glasses as well as new forms of disordered phases of matter.
- Thrust 3: Designing Biomimetic Colloidal Gels. Engineer feedback-controlled colloidal gels with biomimetic behaviors, e.g., self-healing, programmable rigidity, oscillatory response, for smart adaptive materials.
Ultimately, my goal over the next decade is to establish the computational and theoretical infrastructure for closed-loop control of disordered materials, equipping future researchers with blueprints for optimizing them.
Teaching Philosophy and Course Contributions
I teach with empathetic rigor: meeting students where they are, using AI transparently, and training them to verify, explain, and own results they trust.
Philosophy and Approach. My teaching philosophy centers on empathetic rigor: be kind, understand student backgrounds, and pull them into rigorous scientific reasoning. This philosophy is especially crucial as students navigate how to use AI critically and responsibly in their work. To achieve this, I require that every homework assignment include a brief AI note documenting the tools used, prompts, and verification steps. Periodic in-class AI audits then identify hidden assumptions in model-generated solutions, reinforcing the importance of verifying against limiting cases and using mathematical/physical intuition. This approach cultivates the ability to critically evaluate and take ownership of one’s work; a skill increasingly vital as materials science and quantum chemistry rely more heavily on machine learning and computational modeling.
Teaching Experience. At Berkeley, I co-taught undergraduate chemical engineering thermodynamics with Prof. Carlo Carraro, working with students from diverse backgrounds. I designed discussion worksheets to complement his lectures, working through sample problems, limit cases, and dimensional/‘sanity’ checks to build their intuition. Through this approach, we covered thermodynamic postulates through azeotropic phase diagrams and reaction thermodynamics without sacrificing rigor. Since then, embedded in a chemistry department, I’ve further developed my communication skills by engaging with students studying electronic structure theory and spectroscopy. This interdisciplinary immersion has positioned me to communicate fluently across all mathematics–physical sciences interfaces.
Course Contributions. My interdisciplinary background in computational materials science, nonequilibrium statistical mechanics, and energy materials positions me to contribute meaningfully to both foundational and specialized courses. At the undergraduate level, I can teach courses in thermodynamics and phase equilibria, transport phenomena and diffusion, continuum mechanics (solids and fluids), polymer science and soft matter, ceramics and glasses, and electrochemical processes. At the graduate level, I can teach core courses in materials science principles, thermodynamics of materials, and statistical mechanics, as well as specialized courses in glass physics, soft matter physics, and computer simulations of materials. My background also positions me to offer specialized topics courses in computational electrochemistry, nonequilibrium statistical mechanics for energy materials, and deep learning in materials science.
New Course Development. I am passionate about developing courses that bridge theory, computation, and applications across disciplines. I propose three graduate courses that provide fundamental training in nonequilibrium phenomena and applications to energy science and engineering:
Course 1: Nonequilibrium Statistical Mechanics: Classical. This course establishes the foundations for understanding transport and relaxation in classical many-body systems, ranging from soft matter to electrolytes. Beginning with the origin of irreversibility and the second law, the course develops: (i) Irving–Kirkwood theory for transport phenomena, obtaining microscopic expressions for stress, heat flux, and pressure; (ii) Onsager regression hypothesis connecting spontaneous fluctuations to linear response; (iii) Green–Kubo theory for computing transport coefficients from equilibrium correlation functions; (iv) stochastic processes and Fokker–Planck equations for modeling thermal fluctuations; (v) Mori–Zwanzig projection formalism for memory effects and generalized Langevin equations; and (vi) mode-coupling theory for slow structural relaxation. Students will implement these methods in molecular dynamics simulations and derive transport coefficients in materials from first principles.
Course 2: Nonequilibrium Statistical Mechanics: Quantum. This course develops semiclassical and quantum dynamical methods for treating electron-nuclei dynamics beyond the Born–Oppenheimer approximation. Topics include: (i) time-dependent perturbation theory and Fermi’s golden rule for transition rates; (ii) semiclassical approximations (WKB, stationary phase, uniform approximations) and their validity regimes; (iii) path integral formulation of quantum mechanics and imaginary-time methods; (iv) Linearized Semiclassical Initial Value Representation (LSC-IVR) for real-time quantum correlation functions; (v) mixed quantum-classical approaches including Ehrenfest dynamics, trajectory surface hopping (fewest switches, decoherence corrections), and mapping Hamiltonians; and (vi) ring polymer molecular dynamics (RPMD) for computing quantum thermal rate constants and approximating real-time dynamics. Students will implement these methods and critically assess when semiclassical approximations break down.
Course 3: Asymptotics, Numerics, and Informatics for Materials Scientists. This methods course equips materials scientists and engineers with essential mathematical and computational tools, bridging traditional statistical reasoning with modern AI systems. Topics include: (i) asymptotic analysis (boundary layers, multiple scales, WKB theory) for quantum transport, electromagnetic problems, and phase-field models; (ii) numerical ODE/PDE methods including finite element and spectral methods with convergence analysis; and (iii) informatics spanning classical probability and statistics through machine learning, uncertainty quantification, and AI-agent engineering (retrieval-augmented generation, model context protocols, agentic workflows) for experimental data analysis. Readings from The Signal and the Noise by Nate Silver and Patterns, Predictions, and Actions by Hardt and Recht support critical reflection on modeling choices. This course trains students to build, validate, and deploy models while wielding AI critically; all are essential skills for contemporary materials research.
Throughout all three courses, I will implement AI-aware pedagogy: students document AI tool usage, verify model-generated code against analytical limits, and defend their computational choices through dimensional analysis, convergence tests, and comparison with experimental data.
Closing. My goal is to cultivate students who take ownership of their calculations and models, who understand not just what the answer is but why it must be so, and who can defend their work against scrutiny while remaining open to critique. My training brings quantum mechanical rigor, statistical mechanics intuition, and multiscale thinking. Paired with empathetic pedagogy, AI-aware instruction, and a commitment to inclusive advising, I am prepared to contribute to advancing materials research through computational innovation. I aim to train the next generation to be not only technically proficient but also collaborative, curious, and committed to innovation and sustainability through computational materials design.