Glassy Dynamics
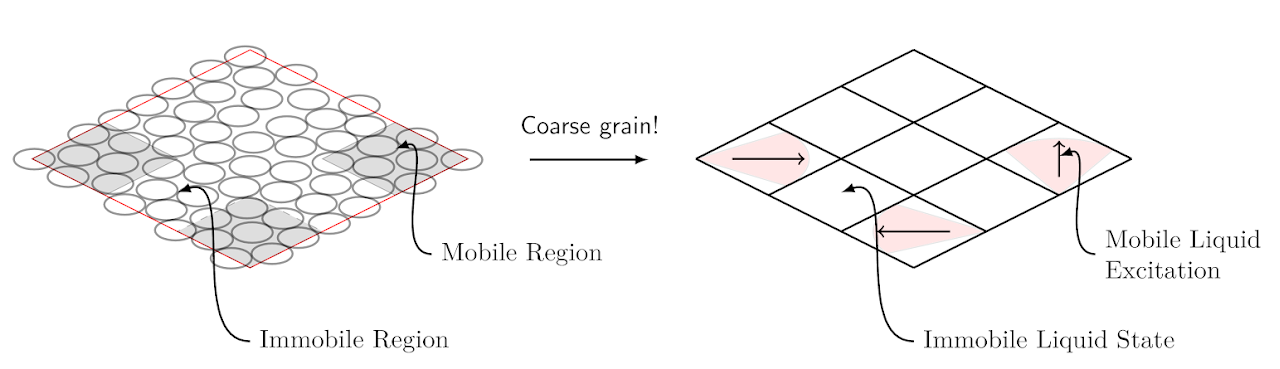
Supercooled liquids are metastable states of glass-forming materials, whose hallmark feature is the dramatic slow down of microscopic dynamics prior to the glass transition. At the mesoscale, supercooled liquids exhibit dynamical heterogeneity, where microscopic reorganization of atoms/molecules are clustered into localized mobile regions and extended “jammed” regions.
Dr. Hasyim’s current research focuses on understanding the origin of glassy dynamics and dynamical heterogeneity as well as their impact on phase-ordering phenomena, such as crystallization and grain boundary annealing.
All works are done under a joint effort with Prof. Kranthi Mandadapu. Another close collaborator on this topic is Prof. Dimitrios Fraggedakis.
Emergent Facilitation and Glassy Dynamics
A central feature of supercooled liquids is dynamical facilitation - the phenomenon where microscopic motion in one region triggers motion in nearby regions, leading to spatially correlated dynamics. Despite its importance in glassy behavior, the microscopic origins of facilitation have remained unclear. Our work presents a theory explaining how facilitation emerges from the interaction between localized bond-exchange events (excitations) and accumulated elastic stresses.
Using linear elasticity theory and Markov processes, Dr. Hasyim and collaborators developed a model that reproduces multiple aspects of glassy dynamics observed in experiments and simulations:
- Stretched exponential decay of relaxation functions
- Super-Arrhenius growth of relaxation timescales with decreasing temperature
- Two-dimensional finite-size effects on relaxation times
- Subdiffusive behavior of mean squared displacement at intermediate timescales
The model also predicts phonon contributions to diffusion and relaxation. When combined with excitation contributions, these produce the characteristic two-step relaxation processes and ballistic-subdiffusive-diffusive crossover behaviors commonly found in supercooled liquids.
This work provides a self-consistent microscopic picture of how the elastic nature of excitations and their interactions leads to emergent facilitation and glassy dynamics. Paper can be found in Ref. [1]
A Theory for Onset Temperature in 2D Supercooled Liquids
The dynamics of glass-forming liquids slow down dramatically below the onset temperature \(T_\mathrm{o}\). Its microscopic origin has been elusive and is often treated as a fitting parameter to distinguish the supercooled regime from the high-temperature regime. Building upon earlier work on a theory of localized excitations, a theory was constructed that allows the study of how inherent states, i.e., the underlying energy-minimizing configurations of the liquid, are stable against excitation fluctuations.
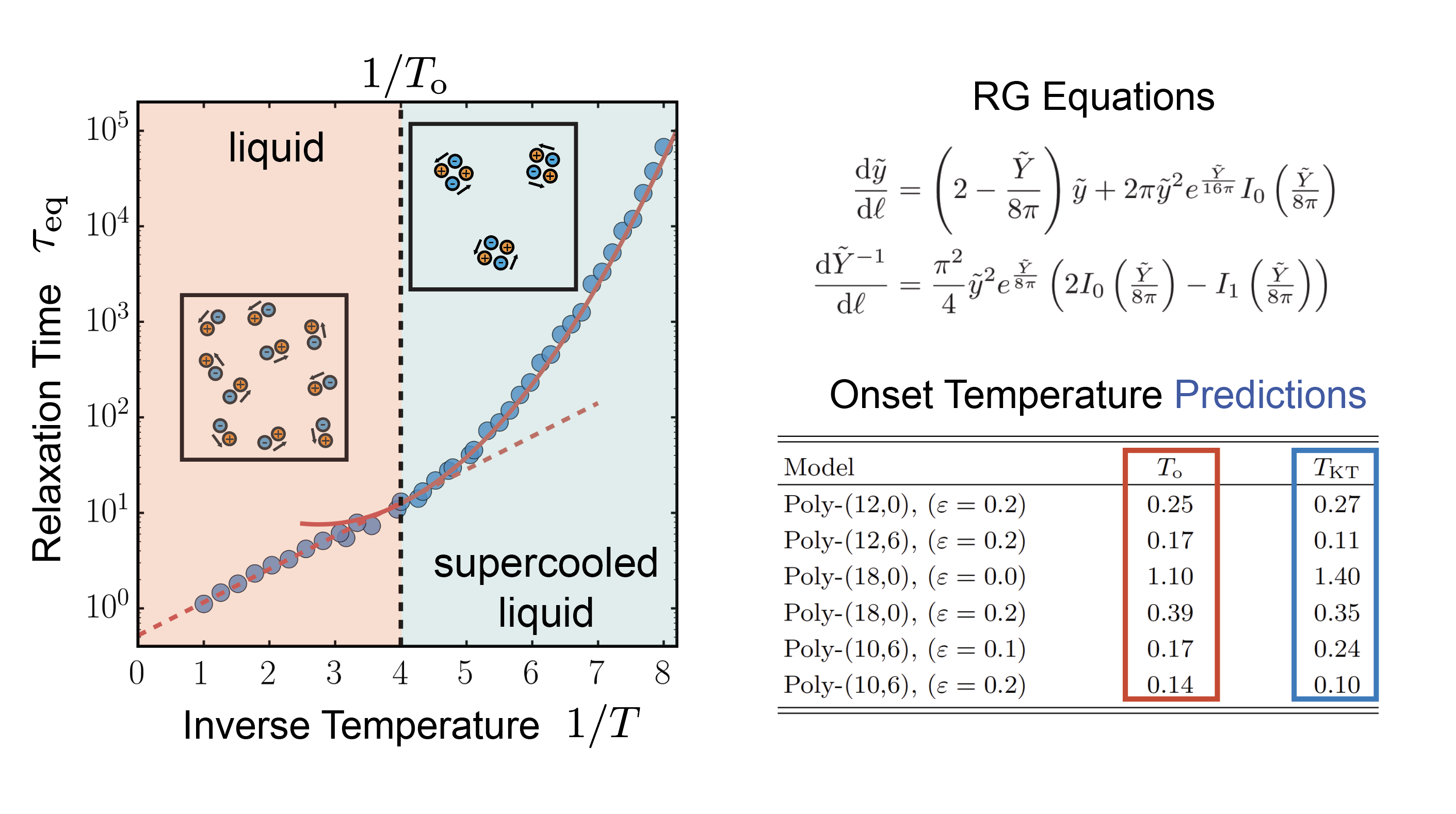
The work was inspired, in particular, by the Kosterlitz-Thouless-Halperin-Nelson-Young (KTHNY) theory of dislocation mediated melting and the work of Moshe and co-workers. The theory predicts that the supercooled liquid is a state where at intermediate timescales, it behaves like a solid filled with pure-shear localized excitations. As temperature is increased, the excitations destabilize to become a pair of “dipolar” excitations, which are able to freely proliferate in numbers. Such proliferation causes the solid to become unstable and macroscopically behave as a fluid.
By repeating the entire renormalization group (RG) analysis of the KTHNY theory, the research team was able to derive equations that can predict the onset temperature with reasonable agreement across various 2D glass formers. In addition, the theory is able to explain the finite-size effects of Mermin-Wagner fluctuations that were recently observed in both experiments and also Kob-Anderson-based molecular models of 2D systems, providing a small but important validation of the theory on literature data.
This work is in collaboration with Dimitrios Fraggedakis. Paper can be found in Ref. [2]
A Theory of Localized Excitations in Supercooled Liquids
To stay mobile at low temperatures, one successful theory of glassy dynamics, known as dynamical facilitation (DF) theory, proposes that microscopic motion is driven by spatially localized excitations, which facilitate the creation and relaxation of nearby excitations in a hierarchical or self-similar manner. Although these excitations are the building blocks of DF theory, their microscopic origin remains unclear.
On the other hand, it is well-known that glassy dynamics also proceed by hopping between inherent states, i.e., energy-minimizing configurations of the potential energy landscape (PEL). Based on this observation, Dr. Hasyim and collaborators constructed a theory which associates excitations of DF theory to hopping events in the PEL.
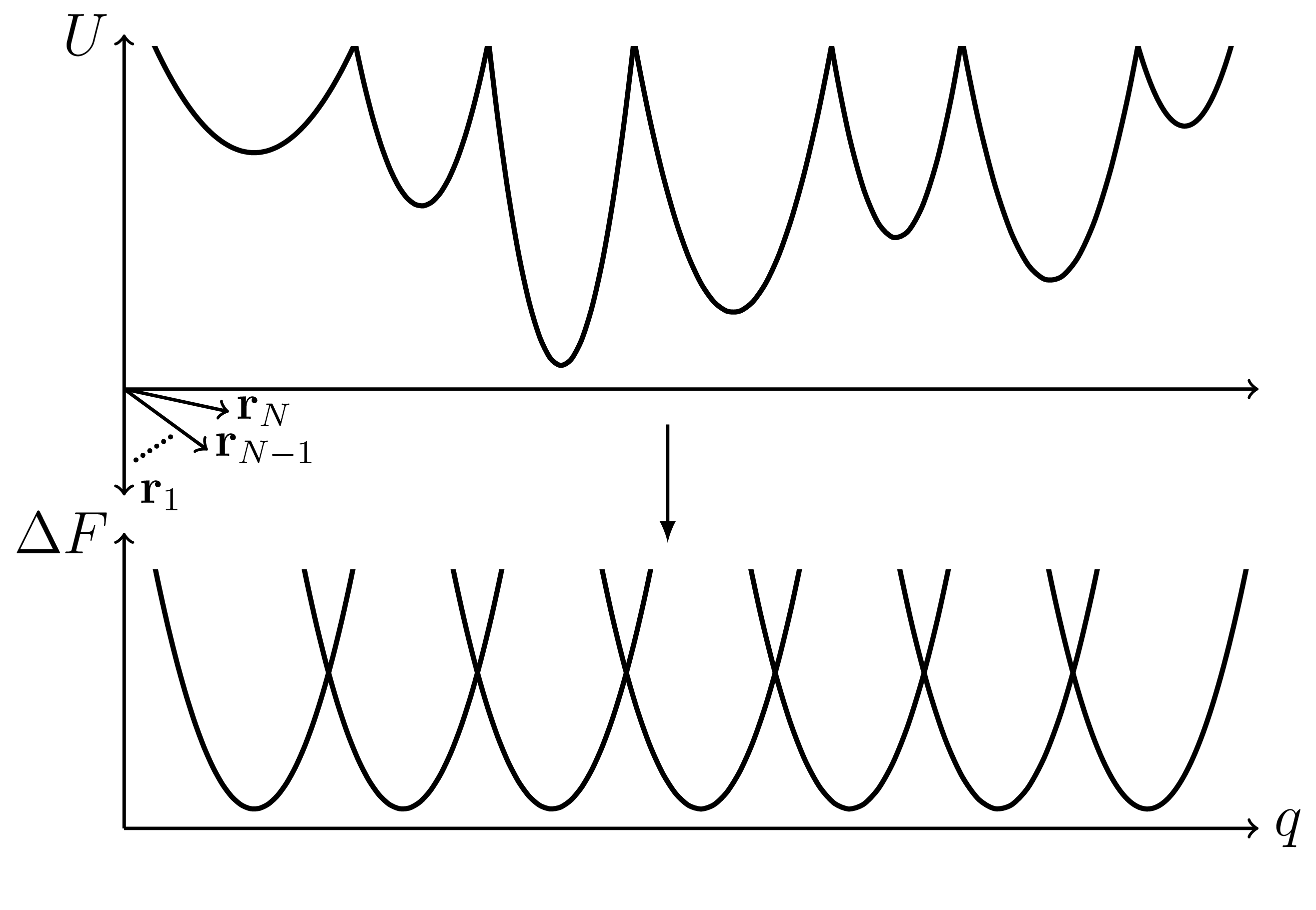
The theory allows derivation of a formula for the excitation energy barrier, denoted as \(J_\sigma\) as a function of elastic and structural properties of the inherent states.
\[ J_\sigma = \lim_{T \to 0} \left[ 6 \pi G^\mathrm{IS} \sigma^2 \frac{\left(\tilde{u}^\ddagger\right)^2\left(1+\tilde{u}^\ddagger\right)^2}{\left(1+2 \tilde{u}^\ddagger\right)^4} \right] \]
where \(G^\mathrm{IS}\) is the shear modulus averaged over all inherent states, \(\sigma\) is the effective particle diameter, and \(\tilde{u}^\ddagger\) is the minimum displacement needed to break an elastic bond. Both \(\sigma\) and \(\tilde{u}^\ddagger\) are computed from the peaks of the inherent-state radial distribution function (RDF).
The project has resulted in two plugins for HOOMD-blue to simulate interacting particle systems with continuous poly-dispersity, ParallelSwapMC and PolydisperseMD. In addition, a new Python package PyGlassTools was developed to perform various calculations needed by the theory.
Paper can be found in Ref. [3]
A Theory for Crystallization vs. Vitrification
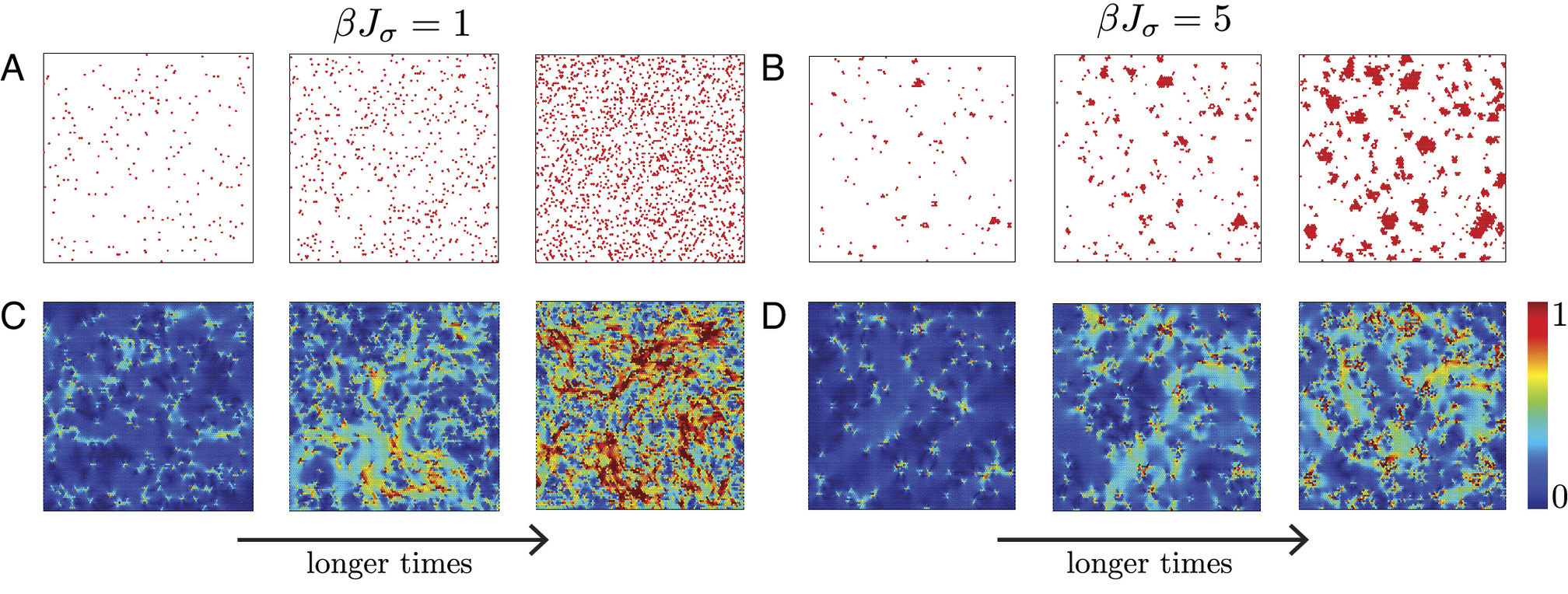
We studied how vitrification competes with crystallization using the Arrow-Potts model (a variant of the Potts model) as a coarse-grained model of supercooled liquids. Near the melting temperature, the model produces poly-crystalline microstructures but at low temperatures, fractal & ramified crystalline clusters were observed instead.
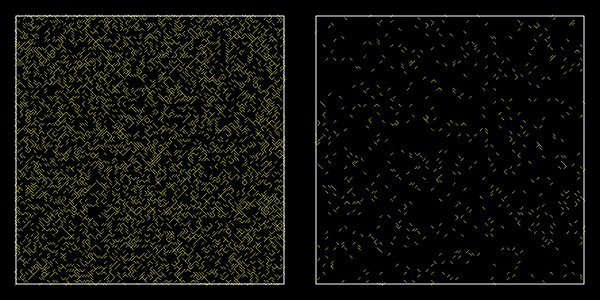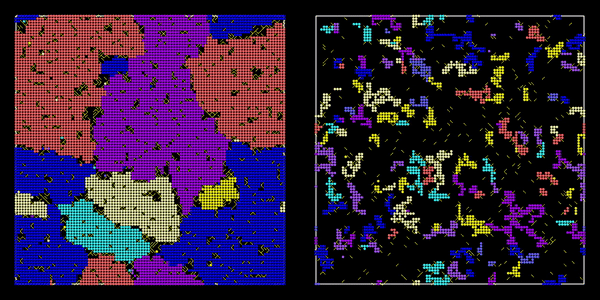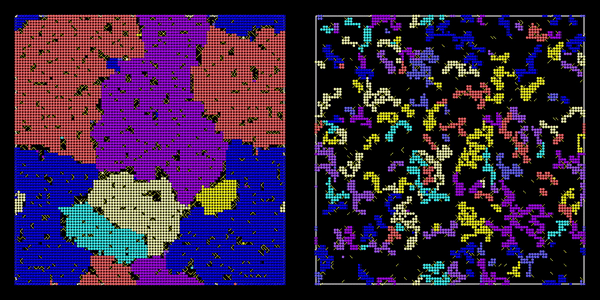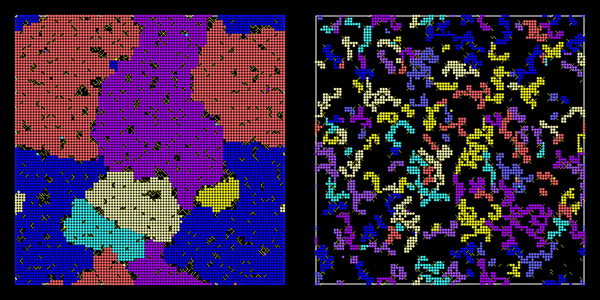
To understand these phenomena, Dr. Hasyim and collaborators used the Kolmogorov-Johnson-Mehl-Avrami theory as a framework to combine three essential theories: (1) the field theory of nucleation, (2) a random walk theory for crystal growth, and (3) the dynamical facilitation theory of glassy dynamics.
The theory relates the overall crystallization timescale \(\tau_\mathrm{xtl}\) with the nucleation time \(\tau_\mathrm{nuc}\) and liquid relaxation time \(\tau_\mathrm{liq}\) by the following formula
\[ \tau_\mathrm{xtl} \sim \left(\tau_\mathrm{nuc} \left(\tau_\mathrm{liq}\right)^{\frac{\alpha d}{2}}\right)^{\frac{1}{\frac{\alpha d}{2}+1}} \]
where \(\alpha\) is a universal exponent characterizing how mobile regions spread across the dynamically heterogeneous liquid.
Paper can be found in Ref. [4]