Machine Learning & Rare Event Sampling
Rare events dominate many microscopic kinetic processes studied in chemistry and physics, including chemical reactions, phase transitions, and protein folding. Despite their obiquity, our current computational resources are unable to simulate nor sample these events in reasonable time and cost. I am broadly interested in developing new algorithms that enable studies of these rare events more efficiently. As it turns out, machine learning (ML) is well equipped for this purpose!
Computing Committor Functions with Neural Networks
The discovery of transition pathways governing kinetic processes at the microscopic level is of fundamental interest in chemistry. Common to these problems is the presence of high-energy barriers, which make the pathway discovery difficult due to the need to sample rare events.
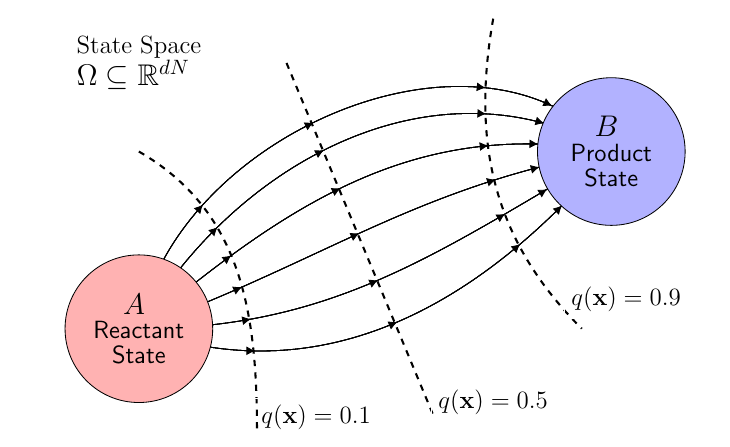
The committor function \(q(\mathbf{x})\), the probability that a trajectory starting from some initial configuration enters the product state before the reactant state, encodes the complete mechanistic details of these pathways, including the reaction rates and transition-state ensembles. Computing the committor function by traditional means is prohibitively expensive, requiring hundreds of trajectories per configuration to yield sufficient estimates along with the need for rare configurations along the transition pathway.
Our work [1] extends the previous approach of Grant Rotskoff and Eric Vanden-Eijnden that combines importance sampling, in which high probability regions of the transition pathway are targeted, and machine learning, in which an artificial neural network approximates the committor function.
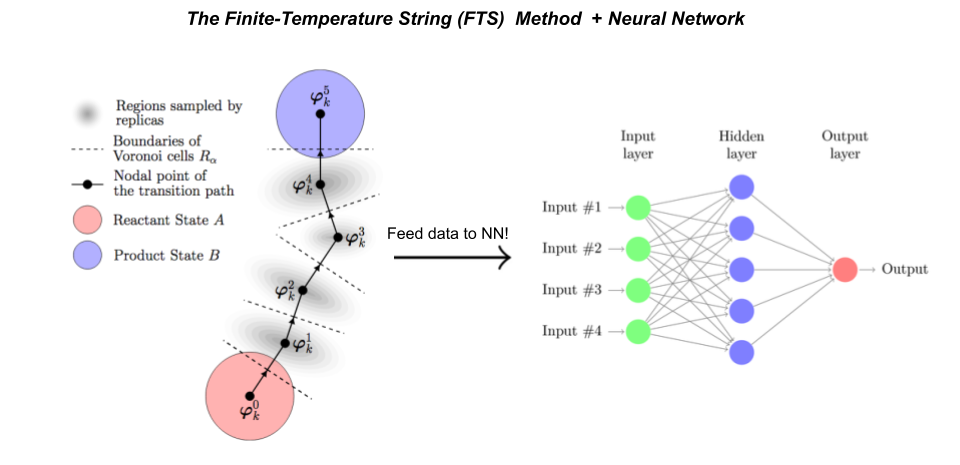
We improved their method by adding two elements: (1) supervised learning, in which sample-mean estimates of the committor function obtained via short simulation trajectories are used to fit the neural network, and (2) the finite-temperature string method, a path-finding algorithm that enables homogeneous sampling across the transition pathway.
We then demonstrate these modifications on low-dimensional systems first, showing that they yield accurate estimates of the committor function and reaction rates. Additionally, an error analysis for our algorithm is developed from which the reaction rates can be accurately estimated via a small number of samples.
This work is done in collaboration with Clay H. Batton and under the supervision of Prof. Kranthi Mandadapu. Code may be found on my Github. Paper can be found in Ref. [1]